
전기/전자 시스템에는 수많은 RLC 성분들이 존재하게 되는데, 이 선형 RLC 성분들의 공진 주파수와 공진점들은 시스템의 성능 및 EMI/EMC 성능에 큰 영향을 미치게 되므로 RLC 성분들의 공진 주파수와 공진점들은 시스템의 성능 및 EMI/EMC성능에 큰 영향을 밈치게 되므로 RLC 선형 회로 해석의 이해는 중요하다.
*EMI/EMC 정의
전자기기에서는 전자파가 발생하고 그 전자파가 다른 기기에 영향을 줄 수 있다.
- 방사(Radiation) : 전자파가 공중으로 전달될 때
- 전도(Conduction) : 전선과 같은 도체로 전달될 때
- Victim : 전자파의 영향을 받는 기기 -Emission : Source에서 전자파가 나오는 것
- Susceptibility : 전자파의 영향을 받는 것
-> EMI(Electromagnetic Interference) : 방사에 의해 다른 기기에 영향을 주는 현상 Source 기기에서 공중으로 전달되는 전자파에(방사) Victim기기가 영향을 받는 전체적인 현상
-> EMC(Electromagnetic Compatibility) : 전자기 적합성, 양립성으로 번역되며, Source와 Victim모두의 전자파환경에 대한 능력 Source로써 전자파를 적게 방출해야 하며 Victim으로서 외부 전자파에 대한 내성을 가지는 것

1. 전기/전자 기초
전기/전자 시스템은 전위차를 의미하는 전압과 그에 따른 전하의 움직임인 전류와의 곱인 전력을 소비하며 동작하게 된다.
이렇게 시스템을 구동 시키기 위해 전력을 공급하는 원천을 전원(Power Source)라 한다.
(1) 전압과 전류
- 전하(Electric Charge)
전하(q)는 물체가 띠고 있는 전기적인 성질 또는 특성
- 전기력(Electric Force)


k는 쿨롱상수라 하며 1/4π€0이다. 여기서 €0는 진공 상태에서의 유전율, 1/4π€0 = 9x10^9Nm^2/C^2
전하 사이에 생성되는 힘을 전기력(Electric Force)라 하고, 전기력은 떨어진 거리의 제곱에 반비례한다.
- 전기장(Electric Field, E)

정전기에서 하나의 점전하에 의해 밀고 당기는 전기력의 힘이 미치는 공간 범위를 전기장 또는 전계라고 한다.

전기장의 크기는 단위 양전하(qo=1)에 미치는 전기력을 의미하는 것으로 위처럼 정의된다.
전기장 E에서 전하 q에 미치는 전기력 힘 F(N) = q x E.
- 전하량(Q, Quantity of Electric Charge)
대전된 물체가 가진 전하의 양, 단위는 쿨롱(C)단위를 사용한다.
(1)-1 전기적 위치 에너지(Electric Potential Energy)
일의 정의인 일 = 힘 X 거리, 힘 Mg에 의해 h 만큼 이동시킬 때의 에너지의 변화를 의미한다.
이렇듯 일은 에너지의 변화를 의미하므로 , 이만큼의 일을 할 수 있는 잠재적인 에너지를 가지고 있다하여 포텐셜(Potential) 에너지라 한다.

전기장 E 내에서 전하 q를 전하 Q로부터 거리 r 만큼 이동시키는데 필요한 에너지로 정의 가능하다.
전기장 E와 전기력 F와의 관계는 F = q X E 이므로, W = qE X r이 되어 전기포텐셜 에너지(U)를 위처럼 정의한다.
즉, 전하 Q로부터 만들어지는 전기장 E내에서 거리 r만큼 떨어진 점전하 q는 위와 같은 전기적 위치 에너지를 가진다.
(1)-2 전위(Electric Potential)

전위는 전하 Q가 만들어내는 전기장 E내에서 위치에 따라 전기적 위치 에너지의 높고 낮음을 표현하기 위한 단위이다.
전위는 전기장 내에서 단위 양전하 1C이 가지는 전기적 위치 에너지와 동일하다.
- 전위의 비교


(1)-3 전압(Voltage)

전압은 어떤 위치의 전위를 기준으로 특정 위치의 전위 차이가 얼마인지를 의미한다.
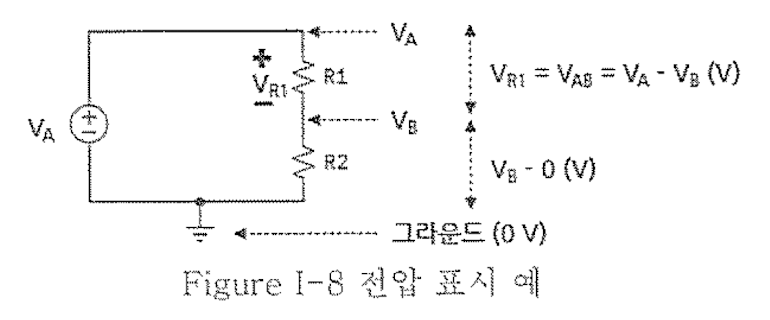
전기/전자 시스템에서는 그라운드라는 기준 전위를 두고 이 전위에서 회로 내 위치의 전위차를 전압으로 사용한다.
(1)-4 전류(Current)
전하가 움직이는 조건에는 전위차가 있어야 하며, 이 흐르는 전하를 전류(Current)라 한다.
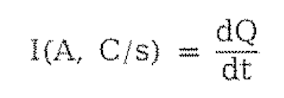
전류 양의 정의는 전하의 단위 시간(1초당) 이동량 또는 단위 시간당 전하량(Q)의 변화량이다.
1A는 1C의 전하량이 1초 동안 흐를 때의 물리량이다.
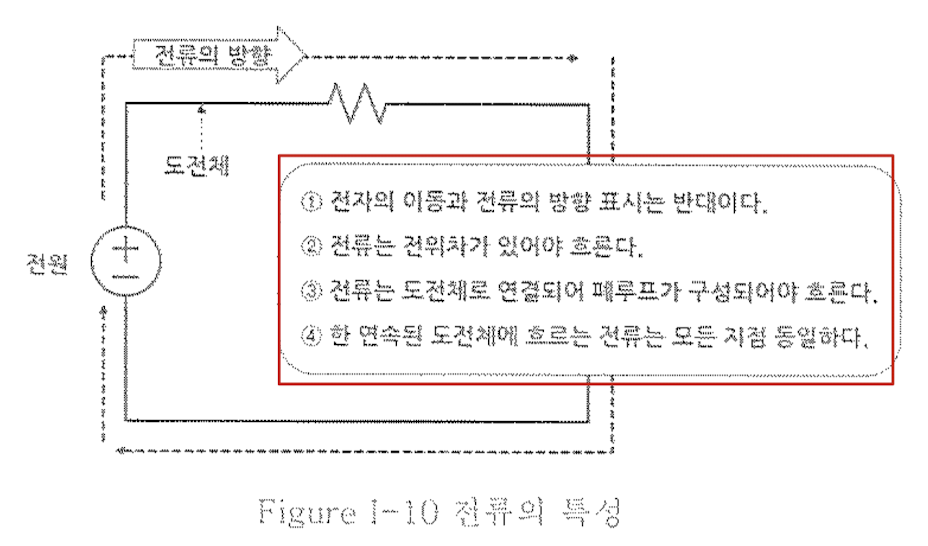
- 전류 흐름의 특성
(1)-5 전기/전자 시스템의 구성과 전력
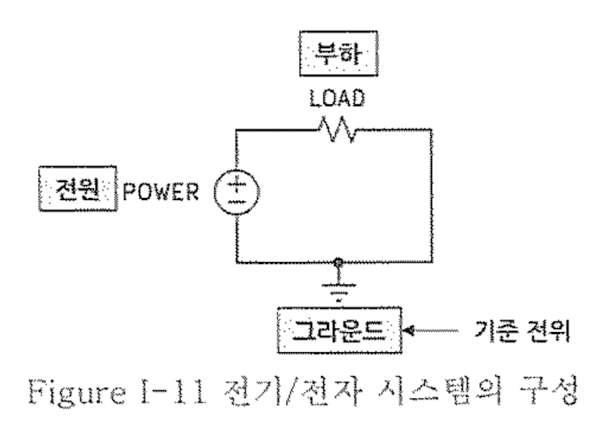
전기 에너지를 공급받아 소모하는 부분을 부하(LOAD)라고 한다.
- 전력(Power)
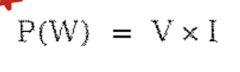
1W는 1V의 전압에서 1A의 전류가 흐르는 에너지이다.
(2) 저항, 커패시턴스, 인덕턴스
(2)-1 저항(Resistance)
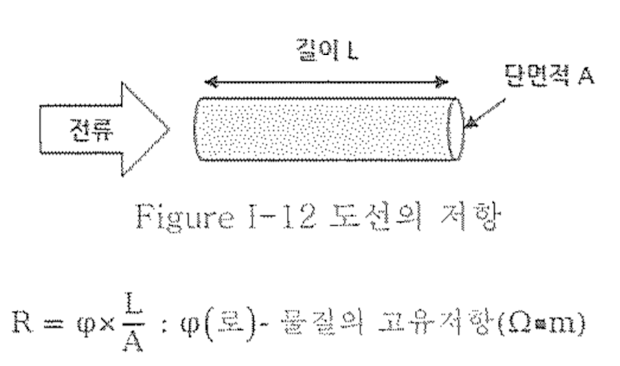
저항 성분은 모든 물체에 존재하는 특성으로 전류의 흐름을 방해하는 성질을 의미한다.
- 옴의 법칙(Ohm's Law)


저항 양단에 걸리는 전압은 그 저항을 흐르는 전류에 비례한다는 법칙
- 소비 전력
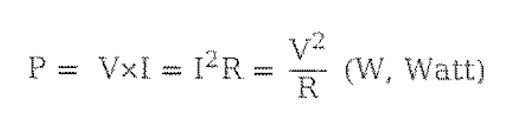
저항은 전기 에너지를 공급받아 에너지를 소모시키는 특성을 가지며, 소모된 전력은 열 에너지로 변환한다.
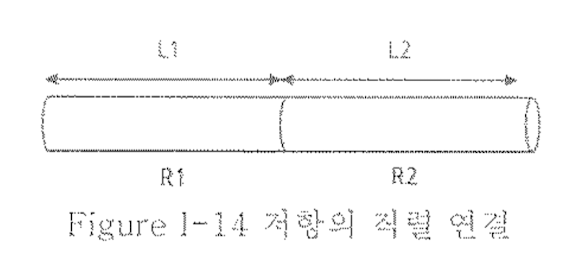
- 저항의 연결
- 직렬연결
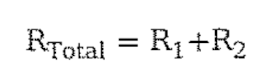
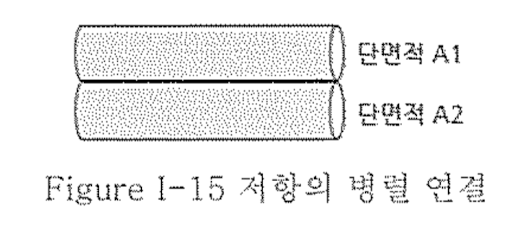
- 병렬연결
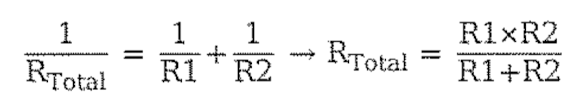
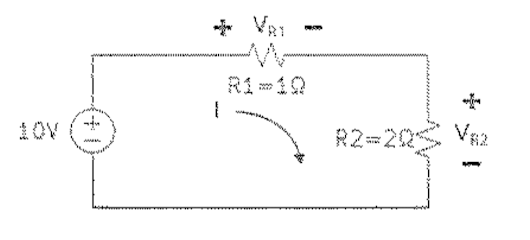
- 옴의 법칙을 이용한 회로 해석 예

(2)-2 커패시턴스(Capacitance, 정전용량) [F]
커패시턴스는 에너지의 소비가 아니라 도전판 사이에 전기장의 형태로 에너지를 저장하는 특성을 가지는데 이런 커패시턴스 성질을 지니도록 만든 소자를 커패시터(Capacitor)라고 한다.
표기 기호는 C를 사용하고 단위는 F(패럿)을 사용하며, 1F는 1V의 전압을 가했을 때 1Q(쿨롱)의 전하량을 축적할 수 있는 능력을 의미한다.

- 전하량(Q)과 커패시턴스의 기본 수식
- 커패시턴스와 전류
커패시턴스 양단 전압의 시간당 변화량 ΔV가 클수록 커패시턴스를 관통하는 전류가 커지고, 직류(DC)와 같이 전압 v(t)의 변화량이 없다면 커패시터를 관통하는 전류는 0이다.
즉, DC는 차단하고 AC는 통과시키는 특성을 가지는데, 시간당 전압의 변화가 큰 고주파의 신호일수록 전류는 커패시턴스를 잘 통과하게 된다는 의미이다.
- 저장된 전기장 에너지
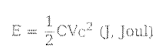
- 커패시턴스 연결
- 직렬 연결

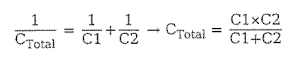
- 병렬 연결
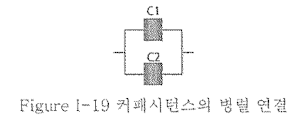
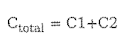
(2)-3 인덕턴스(Inductance, 유도용량) [H]
- 암페어의 법칙과 자기장(Magnetic Field)
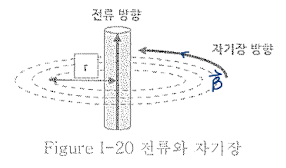
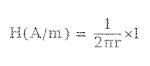
- 자속(Magnettic Flux) B와 투자율(Permeability)
자속 B는 자기력선에 직각인 일정 면적 S(m^2)의 면을 통과하는 자기력선의 수로 정의하며 자기장의 세기를 표현한다.
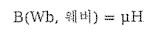
투자율 μ는 물질이 얼마나 자화가 잘 되는 가 즉, 자기장을 얼마나 잘 전달시킬 수 있는가의 정도롤 나타내는 물리량이다.
- 패러데이 법칙과 유도 기전력(Induced EMF)

패러데이 법칙은 도체 주변에 자기장만 있다고 전류가 흐르는 것이 아니라, 자기장(자속)의 변화가 있어야만 유도 기전력이 생성되어 유도 전류가 흐른다는 법칙이다.
유도 기전력은 자기장의 변화로 인해 전류가 흐르게 끔 해주는 전압이 유도된 기전력이며, 시간당 자속의 변화가 빠를수록 큰 전압이 형성된다.
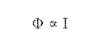
- 트랜스포머의 동작 원리
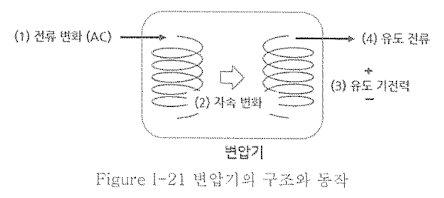
도선의 직접적인 연결 없이도 도선에 자속의 변화가 생기면 기전력이 유도되고, 이는 전류를 만들어 낼 수 있다.
- 인덕턴스(Inductance) [H]
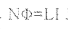
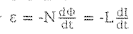
인덕턴스(Inducance)는 전류의 변화에 의해 유도 기전력을 발생시키는 정도의 물리량과 같은 말이며, 유도용량이라고 한다.
도선에 전류가 흐르면 자기장이 생성되고 도선에 교류가 흐르게 되면 자기장의 변화가 발생한다. 이 자기장의 변화는 전류가 변화하는데 반대 방향으로 자기자신에 기전력을 유도하여 결과적으로 전류의 변화를 막는 성질로 작용하게 된다.
이 유도 기전력을 역기전력이라 하고, 인덕턴스에서 빠질 수 없는 성질이다.
- 유도 기전력(Induced Electromotive Force)의 크기
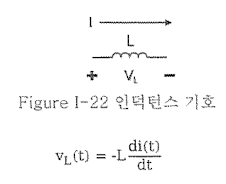
전류의 변화가 없는 직류 DC의 경우 기전력이 생기지 않음을 의미한다.
- 인덕턴스 저장 에너지
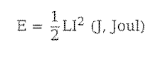
인덕턴스는 전기 에너지를 소비하지 않고 자기장의 형태로 에너지를 저장한다.
- 인덕턴스의 연결
- 직렬 연결
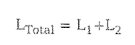
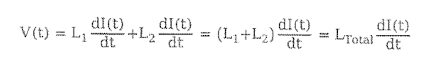
- 병렬 연결
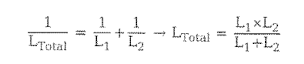
(4) 키르히호프 법칙
(4)-1 1법칙 : 키르호프 전류 법칙(Kirchhoff's Current Law, KCL)
회로 내 한 노드(연결점)로 흘러 들어가는 전류의 합은 흘러 나가는 전류의 합과 같다.
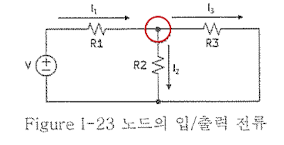
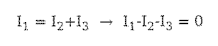
(4)-2 2법칙 : 키르히호프 전압 법칙(Kirchhoff's Voltage Law, KVL)
회로 내 어떤 폐경로에 전류를 회전하며 구한 전압의 합은 0이다는 이론이다.
전류가 루프의 방향으로 소자로 돌아가는 방향을 +로 정의하고 나가는 쪽을 -로 규칙을 정하여, 이에 따라 루프와 만나는 전압 극성에 따른 전압 값들의 합이 0이 된다.
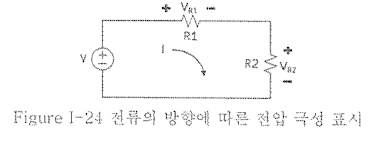
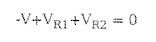
- 키르히호프 법칙을 이용한 회로 해석 예
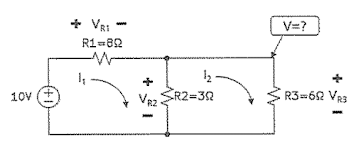
- 루프에 대한 KVL을 구한다.
- 연립 방정식을 푼다.
2. 시스템과 신호의 종류
입력이 하나이고 출력이 하나인 시스템을 SISO(Single Input Single Output)시스템이라 하고, 여러 개의 신호에 하나의 출력인 시스쳄을 MISO(Multiple Input Single Output)시스템이라 한다.

(1) 선형 시스템
(1)-1 LTI(선형 시불변)시스템
시간적으로 변하지 않고 입력에 대해 선형적인 출력을 하는 선형 시스템을 LTI시스템, 선형 시불변 시스템이라 한다.
- 선형 시스템(Linear System)
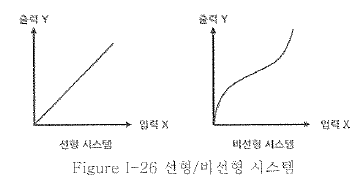
- 선형시스템 조건

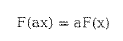
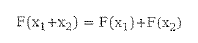
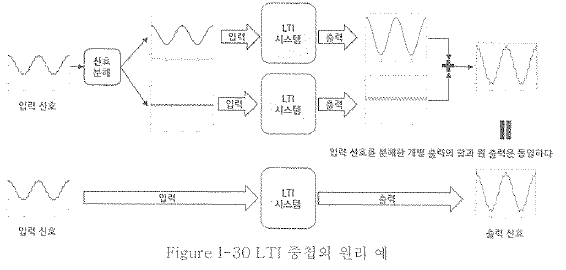
- 중첩 원리와 시스템 해석
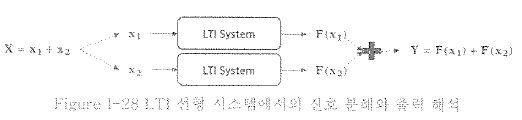
(1)-2 LTI 선형 시스템과 시스템 해석
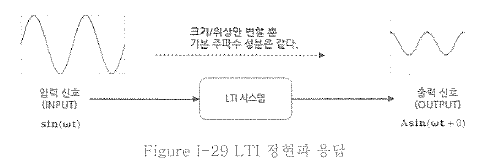
선형 시스템의 중요한 특징은 위 그림처럼 입력에 어떤 주파수 성분이 들어가면, 출력은 입력의 기본 주파수 성분은 바뀌지 않고, 크기(Amplitude)와 위상(Phase,(파이))만 변하는 출력 특성을 가지게 된다.
시스템 해석에 있어 각각의 입력 신호를 분해하여 해석할 수 있다는 특성은 복잡한 신호의 해석에서 필수이기 떄문에, 시스템에 대한 수학적 해석에 있어 모든 시스템은 LTI선형 시스템이라 가정하고 해석을 진행한다.
(2) 전기 특성의 선형성
(2)-1 선형 특성
보통 선형 회로는 RLC 수동 소자로 구성된 회로를 의미하는데, 반도체 소자와 함께 구성되어 있더라도 선형적인 관계를 가지고 있는 구간에서는 선형 회로를 근사해서 해석하기도 한다.
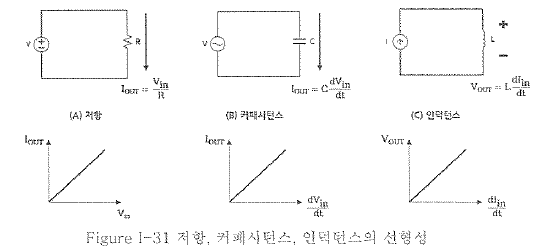
(2)-2 선형 회로의 회로 해석 이론
- 중첩의 원리
- 선형 회로에서의 복수의 전원에 대한 해석 규칙
선형 회로에서 복수의 전원 각각의 입력에 대해 원하는 위치의 전압 또는 전류를 구하여 모두 합하면 최종 출력이 된다.
이때 선형 전기 시스템에서는 각각의 개별 전원의 응답을 구하기 위하여 아래와 같은 규칙이 필요하다.
- 자신이 아닌 다른 전류원은 개방(open)시킨다.
- 자신이 아닌 다른 전압원은 단락(short)시킨다.
이 규칙은 RLC수동 소자들로 구성된 선형 회로에 국한되지만, IC들로 구성된 비선형 회로라고 해도 입력에 출력이 선형인 구간에 적용하여 해석하기도 한다.
- 중쳡의 원리를 이용한 회로 해석의 예
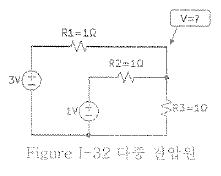

- 테브낭의 등가회로
다수의 전압원, 전류원, 저항으로 구성된 복잡한 회로를 하나의 등가 전압원(V$th$)과 하나의 등가 저항(R$th$)으로 등가회로 표현이 가능하다는 이론이다.
'Study > 회로 설계 및 PCB설계 규칙' 카테고리의 다른 글
| #5 회로 설계 규칙 (0) | 2024.04.22 |
|---|---|
| #4 회로 및 PCB 설계 절차 (0) | 2024.04.15 |
| #3 노이즈(Noise) 기초 이론 (2) | 2024.04.02 |
| #0 규칙으로 배우는 임베디드 시스템 (0) | 2024.03.20 |