전동기의 전류 제어 또는 속도 제어를 위해 사용된 비례적분 제어기에서 원하는 응답특성을 얻을 수 있도록 이득을 선정하는 방법에 주파수 응답 특성을 분석해 원하는 응답 특성을 갖도록 이득을 선정 해야한다.
이러한 제어계 설계 시에는 통상 안정성, 응답성, 정상상태 오차의 세 가지 요소가 고려되어야 한다.
0. 주파수 응답(Frequency Response) 특성이란?

주파수 응답이란 어떤 선형 시스템에 일정한 진폭을 갖는 정현파 입력 신호 r(t)를 인가했을 때 정상상태에서 어떠한 출력 c(t)를 내는지 보이는 것이다.

입력 신호의 주파수에 따라 그 출력의 크기와 위상이 입력 신호와 달라질 수 있는데, 주파수 응답은 그 차이의 정도를 보여주는 것이다.
전달함수 G(s)에 따라 output이 달라진다.
(1) 주파수 전달함수

시스템의 전달함수 G(s)에서 s를 jw로 놓고, 다양한 주파수 w에 따라 계산된 G(jw)의 크기와 위상이 시스템의 주파수 응답이 된다.
시스템의 주파수 응답은 주파수 이득(주파수 전달함수의 크기)과 위상차(주파수 전달함수의 각도[phi])로 이루어진다.
전달함수는 입력과 출력의 비이므로 주파수 전달함수의 크기와 각도가 주파수 이득과 위상차가 된다.
이러한 응답 특성을 그림으로 표현한 것이 보드 선도(Bode Plot)이다.
(2) 벡터 궤적
벡터 궤적은 주파수 함수에서 w를 0에서 무한대까지 값을 변형시키면서 그 크기와 위상을 표혀한 것
1. 비례요소
G(s) = K => G(jw) = K
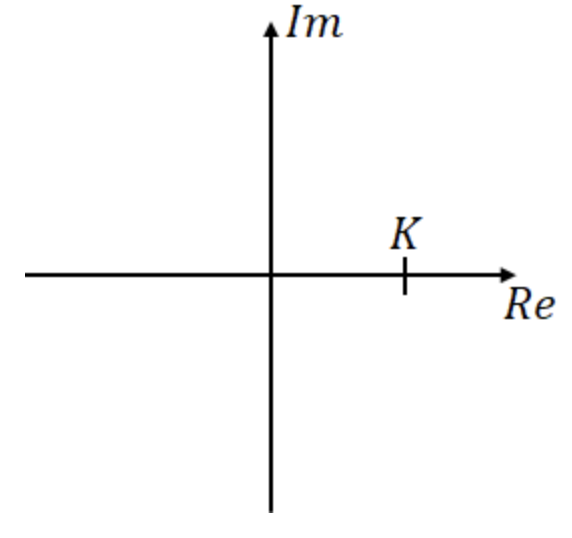
jw항이 없어서 K가 양수라면 복소평면에 위처럼 표현된다.
2. 미분요소
G(s) = s => G(jw) = jw

w항이 있어 위처럼 Im축에 그려진다.
3. 적분요소
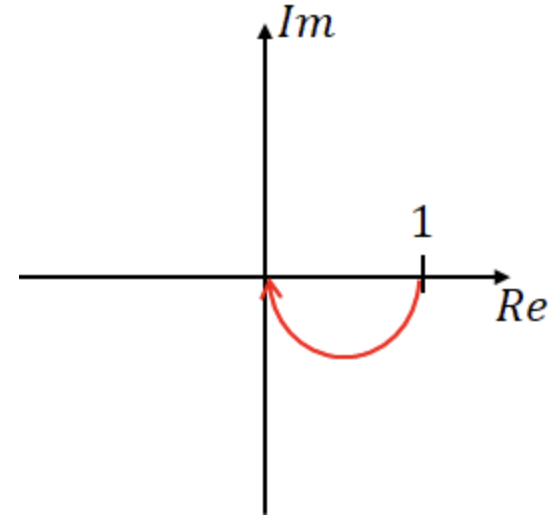
G(s) = 1 / s => G(jw) = 1 / jw = - j * 1 / w

w = 0에서 무한대이고, w가 무한대로 갈 수록 0으로 수렴한다.
4. 1차 지연요소
LPF형태를 지연필터 형태로 표현할 수 있다.


위의 방식과 같이 주파수이득과 위상을 구하면 위와 같이 나타낼 수 있다.
벡터궤적은 wT의 크기의 변화에 따라 바뀐다.

5. 2차 지연 요소
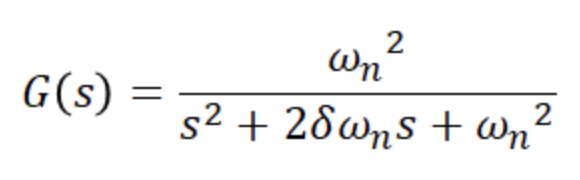
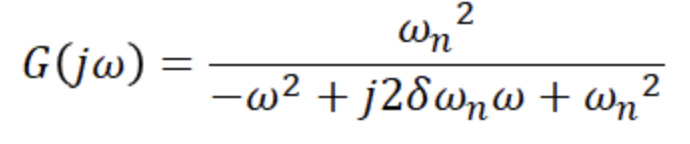
분모 분자를 wn으로 나누고, wn은 고유 진동 각주파수로 변화하지 않는 값이므로 w/wn을 람다로 치환한다.
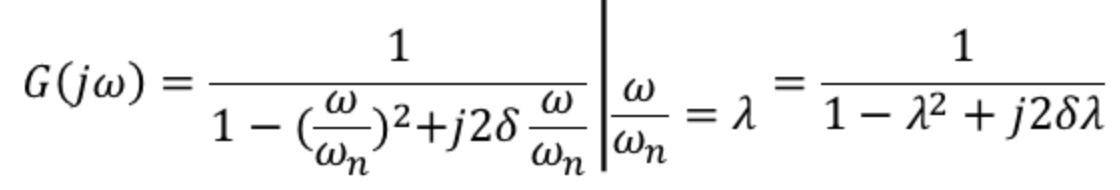
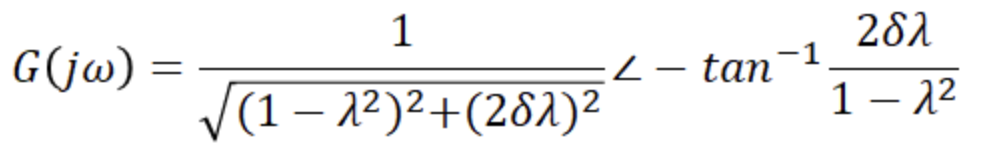
벡터 궤적을 보기 위해 람다를 0,1,무한대로 보내고 그래프를 그리면,
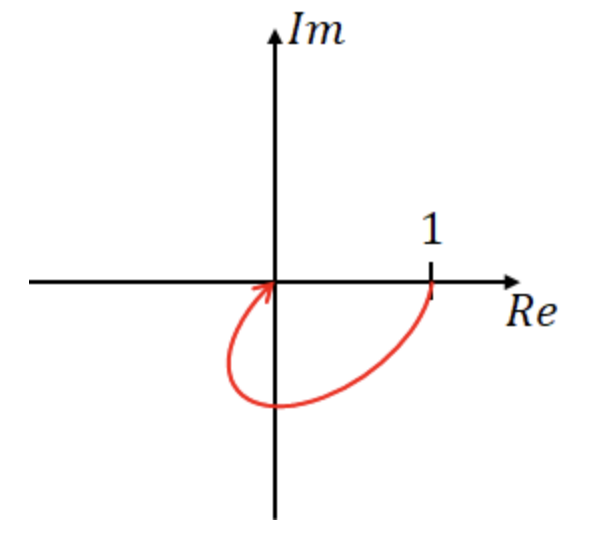
6. 부동작 요소
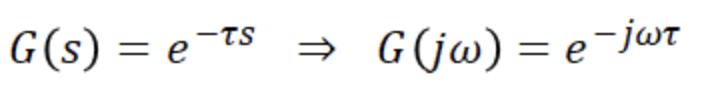
wt의 값에 따라 벡터궤적이 바뀐다.
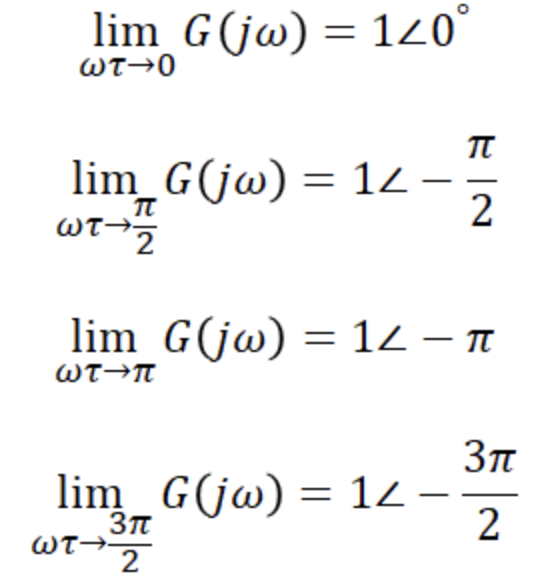
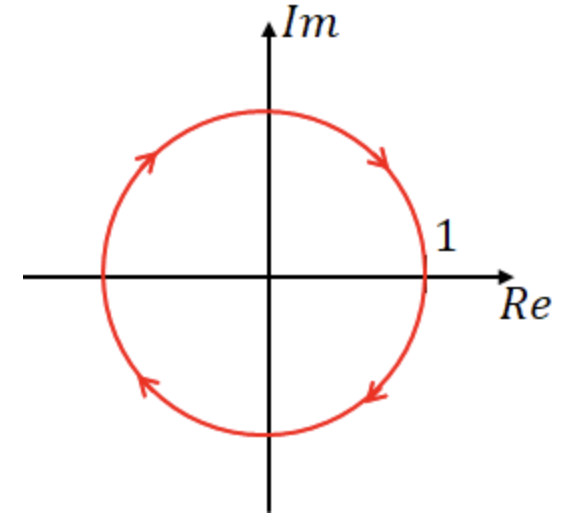
크기는 일정하고 위상만 변하는 벡터궤적이 나타난다.
(3) 보드선도(Bode Plot)
Bode Plot은 주파수 응답을 나타내는 그래프로 입력 주파수에 따른 크기 응답과 위상 응답 두 개의 그래프로 구성된다.
(가로축은 입력 주파수를 나타태고 로그스케일이다.)
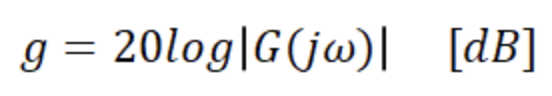
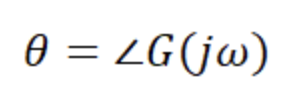
크기 응답은 주파수 전달함수에 밑이 10인 로그함수 형태이고 위상응답은 그 phase다.
1. 비례요소
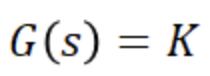
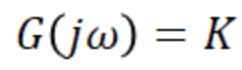
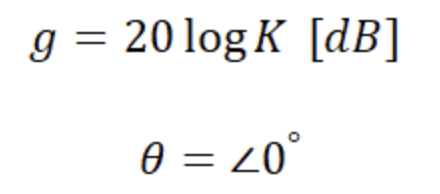
비례요소에 따른 크기 및 위상응답으로 주파수 변화에 관계없이 크기 및 위상 응답은 일정한 값을 가진다.
2. 미분요소
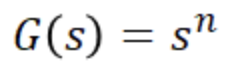
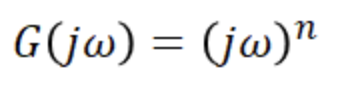

미분요소에 따른 크기 및 위상응답으로,
여기서 보드선도는 가로축을 로그스케일을 사용하기에 크기 응답의 계수인 20n이 보드선도의 기울기이다.
3. 적분요소
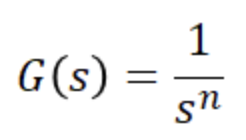
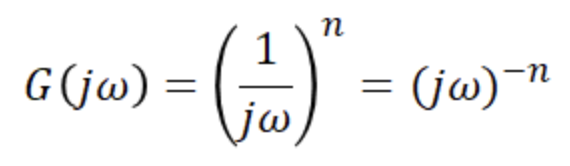

4. 1차 지연 요소

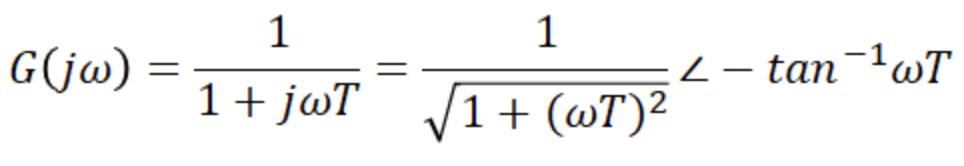
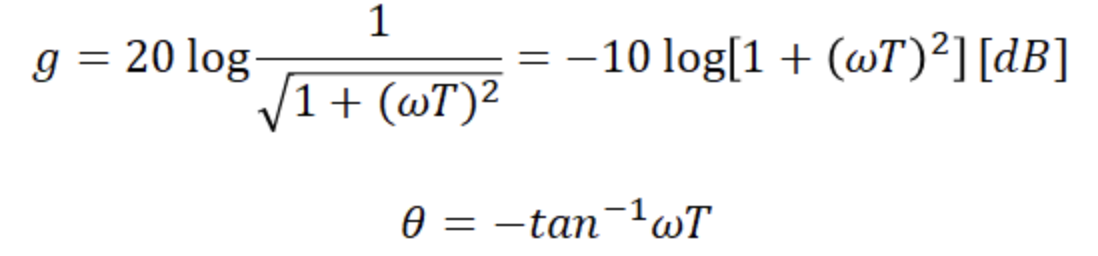
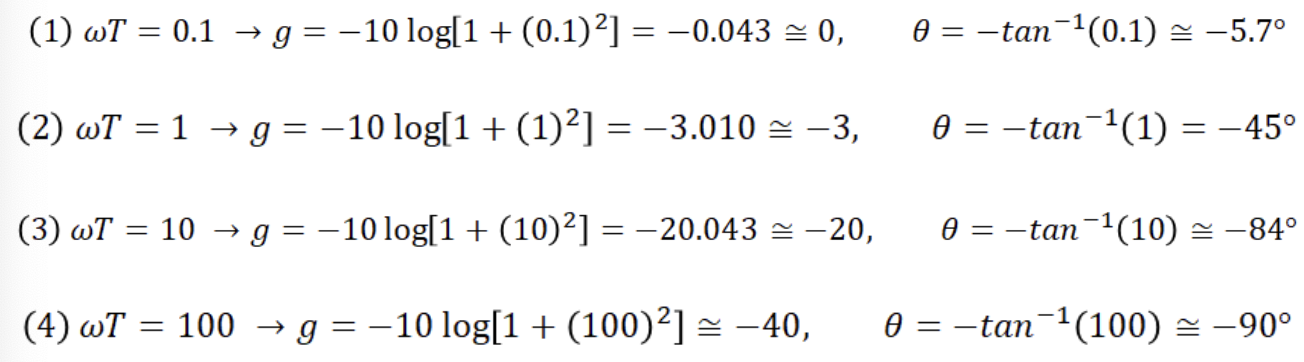
wT에 0.1, 1, 10, 100으로 10의 거듭제곱 꼴의 값을 대입하며 크기와 위상 응답을 구한것이다.
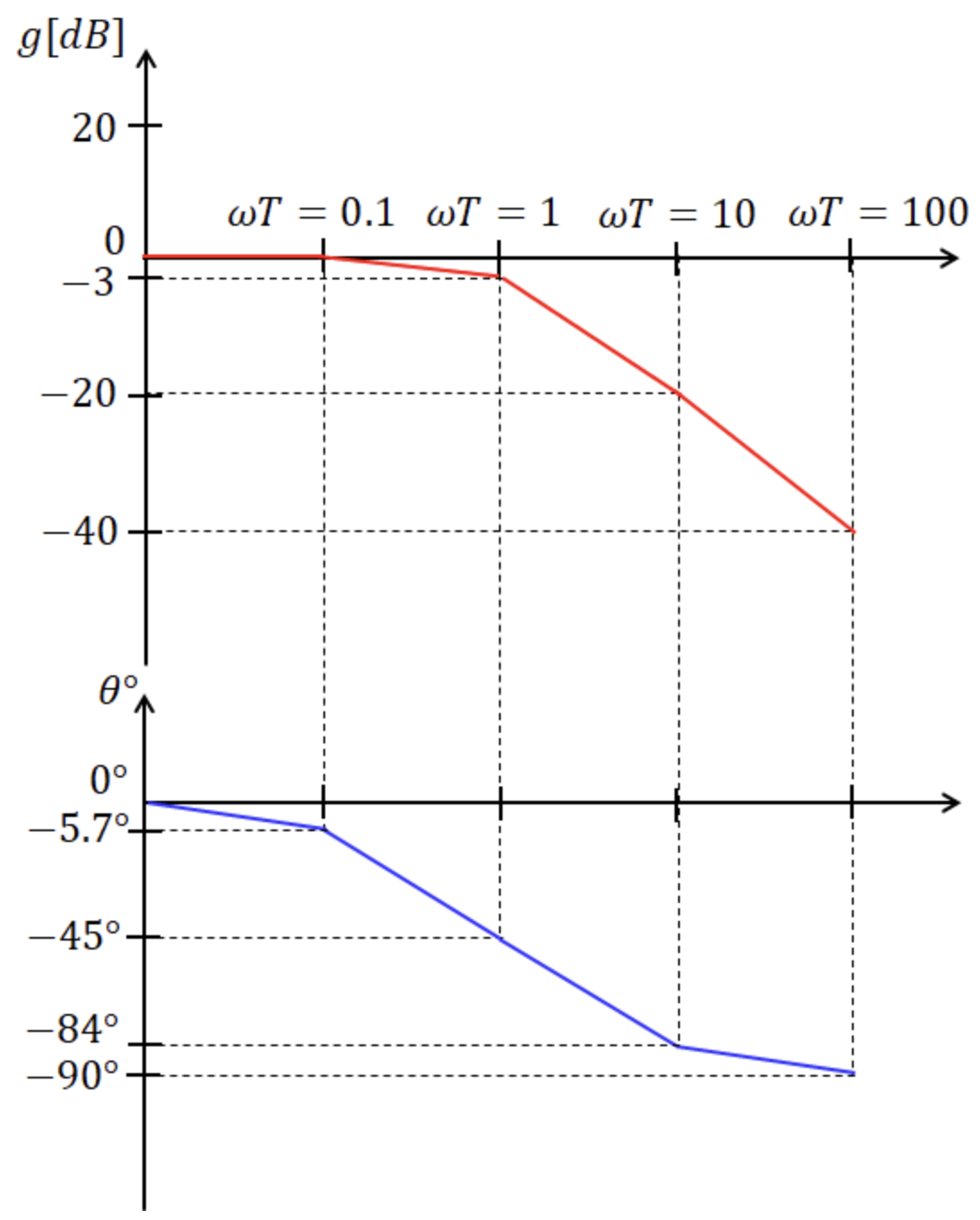
위와 같이 보드선도에서 크기 응답을 나타낸 곡선을 이득 곡선(gain margin), 위상 응답을 그린 곡선은 위상 곡선(Phase margin)이라고 한다.
그래프를 보면 wT가 1인 지점에서 크기 응답의 값이 급격하게 변화하고 있다.
이런 급격한 변화가 생긴느 주파수를 절점주파수라고 한다.
- 절점 주파수 : 크기 응답이 급격하게 변화가 생기는 지점을 말하며 실수부와 허수부가 같아지는 지점에서 발생.
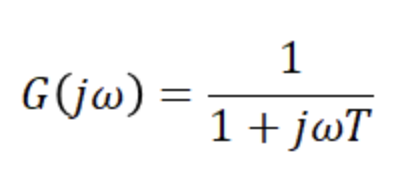
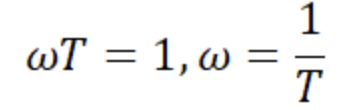
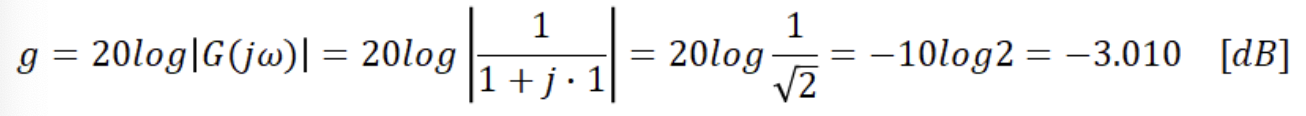
1. 안정성(Stability)
폐루프 제어시스템의 안정성은 폐루프 전달함수에서 특성방정식의 근의 s-평면상에서의 위치를 통해 알거나 특성방정식의 각 항의 부호를 조사하는 Routh-Hurwitz안정성 판별법을 통해 알 수 있다.
또한 극좌표상에서의 개루프 시스템의 주파수 특성을 이용하는 나이키스트(Nyquist) 안정성 판별법으로도 안정도를 파악할 수 있다.
여기서 설명할 주파수 응답을 통한 제어기 설계 시에 폐루프 제어시스템의 안정도는 개루프 전달함수에 대한 주파수 응답 특성, 즉 보드 선도에서 이득 여유(Gain Matgin) 와 위상 여유(Phase Margin)를 살펴보고 판달할 수 있다.
2023.03.10 - [Study/Motor Control] - Nyquist[나이퀴스트]와 Bode Plot[보드선도] 안정도 판별법
Nyquist[나이퀴스트]와 Bode Plot[보드선도] 안정도 판별법
jgewjsrhdms.tistory.com
=> 위 포스팅을 읽고 밑을 보면 이해하기 쉽다.
(1) 이득 여유(Gain Margin)
시스템이 불안정해지기까지 시스템의 크기 응답을 얼마만큼 증가시킬 수 있는가를 나타낸다.
- 제어계의 안정조건 두가지
1. 개루프 주파수 전달함수가 음의 실수축과 만나는 점이 -1보다 커야한다.
2. 개루프 주파수 전달함수의 크기가 1인 점에서 음의 실수축 간에 형성되는 사이각이 180도 보다 작아야한다.
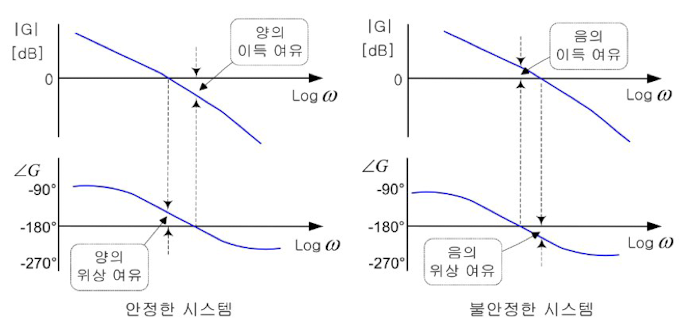
위의 그림에서 보드 선도와 같이 위상 phi = 180도가 되는 위상 교차 주파수(Crossover Frequency)에서 이득 |G|가 0dB보다 작으면 양의 이득 여유를 갖으며, 이 경우 시스템은 안정하다.
오른쪽 그림에 보이는 보드선도에서는 음의 이득 여유를 가짐으로 시스템은 불안정하다.
(2) 위상 여유(Phase Margin)
이것은 시스템이 불안정해지기까지 위상 응답이 얼마나 지연될 수 있는가를 나타낸다.
위의 왼쪽 그림과 같이 이득 |G| = 0dB가 되는 이득 교차 주파수에서 위상 phi가 -180도 보다 크면 양의 위상 여유를 갖으며, 이 경우 시스템은 안정하다.
그러나 오른쪽 보드 선도에서는 음의 위상 여유를 가짐으로 시스템은 불안정하다.
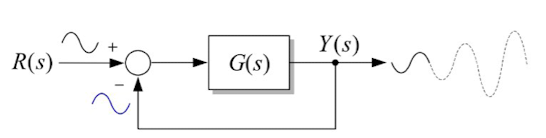
예를 들어, 단위 부궤한 제어(Unit Negative Feedback Control)시스템에서 어떤 각주파수 w의 입력에 대해 출력의 크기, 즉 이득 |G| = 1이 되었을 때, 위상 각GH가 180도로 지연되었다고(즉, 위상여유 = 0) 가정해보면.
이 경우에 Y(s)와 R(s)와의 위상차는 180도가 되어 부궤환 제어인 폐루프 시스템은 오히려 정궤한(Positive Feedback) 제어가 된다.
따라서 계속적으로 출력이 증폭하게 되어 시스템이 불안정해진다.
불안정 시스템은 응답이 지속적으로 진동하거나 발산한다.
=> 이득 여유와 위상 여유는 시스템이 불안정해지기 까지 증가시킬 수 있는 이득과 위상 지연의 여유 양을 의미하며 시스템의 상대적 안정도를 알 수 있다.
폐루프 시스템이 안정하려면 이득 여유와 위상 여유는 양이어야 한다.
그러나 둘이 양의 값으로 너무 큰 경우에는 시스템의 응답성이 늦어진다.
일반적으로 이득 여유는 2~10dB 정도, 위상 여유는 30~60정도인 것이 좋다.
통상적으로 시스템의 이득을 키우면 위상여유가 작아진다.
2. 응답성(Response Time)
속도나 전류 등을 제어하는 시스템에서 지령 값을 추종하는 응답 속도는 다를 수 있다.
이런 응답 속도는 통상 폐루프 시스템의 제어 대역폭(Bandwidth)으로 표현된다.
대역폭은 rad/s 또는 Hz의 단위로 표시하는데, 200Hz의 제어 대역폭을 갖는 시스템은 100Hz의 시스템보다 응답속도가 2배 빠르다고 볼 수 있다.
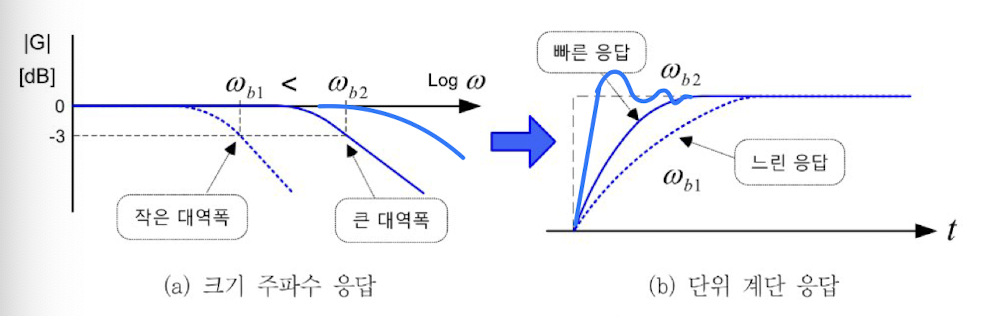
제어 대역폭이 넓으면 빠른 응답 속도를 얻을 수 있지만, 넓어질수록 피드백 제어를 위해 궤한된 물리량에 포함된 잡음의 영향이 커지게 되어 시스템이 불안정해질 수도 있다. => trade off
- 대역폭(Bandwidth)이란?
대역폭은 시스템이 입력 정현파 신호를 얼마나 잘 쫒아가는가를 나타낸다.
즉, 대역폭은 입력 신호를 재생할 수 있는 능력을 표현하는 지표라 할 수 있다.
대역폭은 시스템의 폐루프 주파수 응답으로부터 알아낼 수 있다.
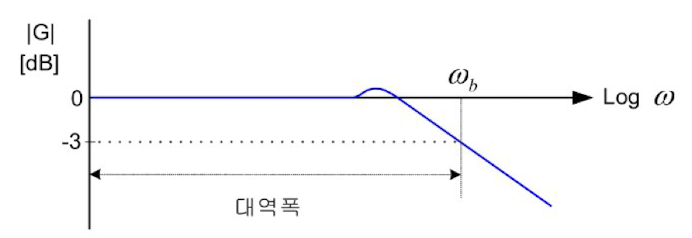
폐루프 주파수의 응답의 크기가 직류 이득(즉, w = 0에서 크기)의 0.707(= -3dB)로 작아지는 주차수를 차단 주파수(Cutoff Frequency)또는 모서리 주파수라 하는데, 시스템의 대역폭은 Wb까지의 주파수 범위를 말한다.
대역폭 범위 내의 주파수를 갖는 정현파 입력 신호는 재생할 수 있다.
(Wb보다 낮은 주파수의 정현파 입력 또는 지령은 잘 추종하지만, 그보다 높은 주파수의 입력은 잘 추종하지 못한다.)
3. 정상상태 오차(Steady State Error)
정상상태 오차는 폐루프 시스템의 오차 식에 최종값 정리(Final Value Theorem)를 적용하면 쉽게 알 수 있다.
그 최종 값이 작을수록 오차가 작은 것인데, 만일 그 최종 값이 0이라면 정상상태 오차는 0이다.
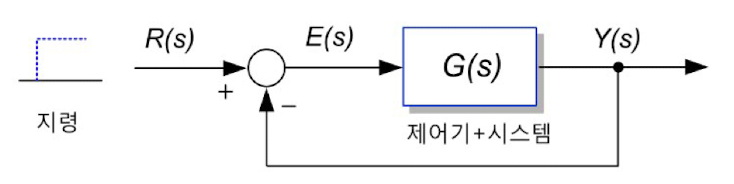
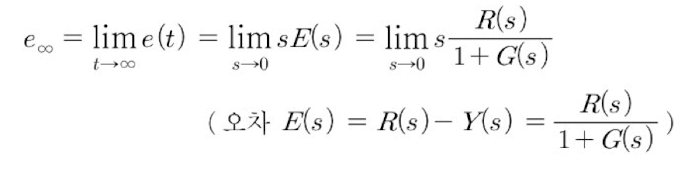
이로부터 단위 계단 입력 즉, r(t) = 1 (-> R(s) = 1/s )을 인가한 경우 발생하는 정상상태 오차 e는 다음과 같다.
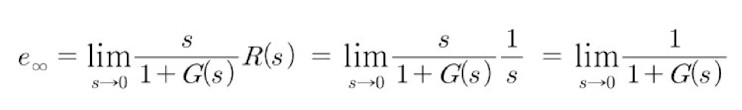
이 경우 정상상태 오차는 제어 대상 시스템 G(s)의 형(Type)에 따라 달라진다.
즉, G(s)에 포함된 적분기(1/s)의 개수에 따라 달라진다.
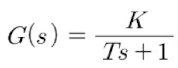
예를 들어, 전달함수가 왼쪽 그림과 같이 표현되는 적분기가 없느 Type 0의 시스템을 생각해보면. 이 경우의 정상상태 오차는
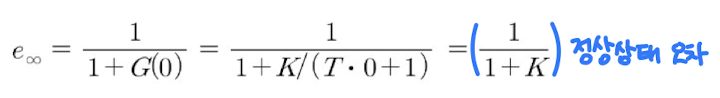
이 되어 영이 아닌 정상상태 오차가 존재하고, 그 오차의 크기는 직류 이득 G(0) = K에 따라 달라짐을 알 수 있다.
=> 시스템 내부에 적분기 (1/s)가 존재하면 단위 계단 지령에 대해 정상상태 오차가 발생하지 않는다.
'Study > Feedback System' 카테고리의 다른 글
| 이산 시간 Low pass filter 코드 변환 (0) | 2024.09.26 |
|---|---|
| Nyquist[나이퀴스트]와 Bode Plot[보드선도] 안정도 판별법 (0) | 2023.03.10 |
| PID control (0) | 2022.08.02 |